De nouvelles descriptions mathématiques pour garder une longueur d’avance sur les courbes
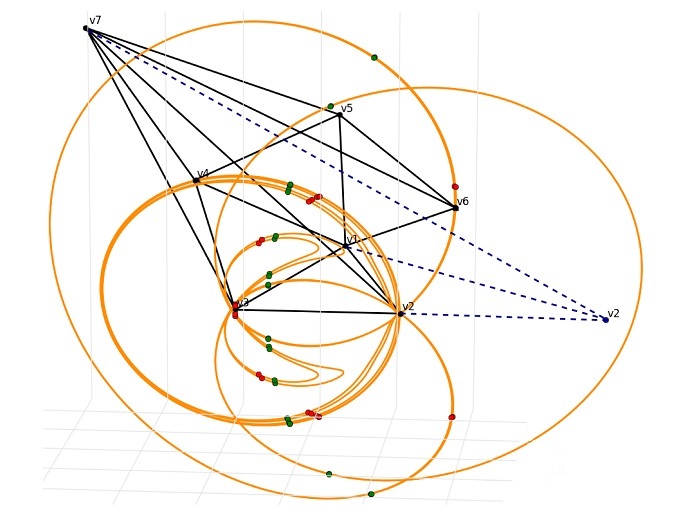
Les mathématiques – formellement, l’étude des nombres, des formes et de l’espace – nous procurent un langage dont nous nous servons pour décrire le monde qui nous entoure. La géométrie est la discipline qui traite des relations entre les points, les lignes, les courbes et les surfaces. Avec le soutien des actions Marie Skłodowska-Curie (AMCS), le projet ISOPARAMETRIC s’est attaché à étudier une classe spécifique de surfaces (les hypersurfaces isoparamétriques) qui ont suscité un intérêt considérable au cours des deux dernières décennies.
Des courbes partout autour de nous
Le coordinateur du projet, Alberto Enciso, de l’Institut des sciences mathématiques – ICMAT, explique: «En gros, une hypersurface isoparamétrique est une forme géométrique lisse qui se courbe partout de la même manière. Un cercle, un plan et la surface d’une sphère ou d’un cylindre sont les exemples les plus élémentaires d’hypersurfaces isoparamétriques. Ces objets se retrouvent dans l’espace à 2 et 3 dimensions et sont maximalement symétriques – les objets ont la même apparence d’un nombre maximal de points de vue différents.» Alberto Enciso poursuit en évoquant ce qui se passe lors du passage à des dimensions supérieures. «Nous trouvons des hypersurfaces isoparamétriques très intéressantes et plutôt complexes qui ne sont pas aussi symétriques qu’on pourrait le penser.» Les surfaces isoparamétriques sont présentes dans toute la physique et les mathématiques. Par exemple, les formes d’équilibre des fluides autogravitants en mécanique des fluides sont des surfaces isoparamétriques et il existe un lien inattendu entre les nombres premiers et les objets connexes appelés feuilletages isoparamétriques. Miguel Domínguez-Vázquez, boursier de l’AMCSA, désormais à l’Université de Saint-Jacques-de-Compostelle, a étudié ces surfaces intrigantes sous différents angles.
La solution à de nombreux problèmes
De nombreux problèmes scientifiques sont modélisés par des équations différentielles partielles (EDP) impliquant des dérivées, des taux de changement d’une variable par rapport aux autres. Certaines de ces équations peuvent ne pas avoir de solutions, comme c’est le cas de nombreux problèmes de valeurs limites surdéterminées des EDP, un domaine de recherche essentiel de ces 50 dernières années. Le terme «surdéterminé» signifie qu’il y a plus d’équations que d’inconnues et qu’elles n’ont donc souvent pas de solution. Alberto Enciso et Domínguez-Vázquez ont fait évoluer ce domaine important: «Parmi nos principaux résultats, nous avons prouvé l’existence de solutions aux problèmes de valeurs limites surdéterminées des EDP dans des contextes très généraux et montré que, dans certaines circonstances, ces solutions sont liées aux hypersurfaces isoparamétriques. En outre, nous avons développé une compréhension complète des (hyper)surfaces isoparamétriques dans certains espaces importants non plats de trois dimensions, montrant que dans ces cas, les surfaces isoparamétriques sont effectivement maximalement symétriques.» Les résultats d’ISOPARAMETRIC devraient trouver une application future dans l’obtention de résultats d’existence ou de non-existence pour les hypersurfaces isoparamétriques en général, ainsi que pour permettre une compréhension complète des surfaces isoparamétriques dans ce qu’on appelle les «espaces homogènes de dimension 3». Ils seront probablement aussi utilisés dans le domaine des flux de fluides incompressibles.
Une nouvelle façon de considérer les hypersurfaces isoparamétriques
Les hypersurfaces isoparamétriques ont généralement été étudiées à l’aide de méthodes algébriques et de géométrie différentielle, alors que la géométrie différentielle classique traite des courbes et des surfaces dans l’espace euclidien 3D. Domínguez-Vázquez conclut: «La chose la plus excitante dans ce projet a été de lancer une nouvelle ligne de recherche qui nécessitait l’apprentissage d’un domaine différent des mathématiques. ISOPARAMETRIC a étudié les hypersurfaces isoparamétriques et les objets connexes en combinant ces méthodes “classiques” avec des techniques plus analytiques.» De toute évidence, une courbe d’apprentissage abrupte a conduit à des résultats importants concernant ces surfaces intrigantes qui se courbent de la même manière partout.
Mots‑clés
ISOPARAMETRIC, hypersurfaces isoparamétriques, mathématiques, équations différentielles partielles (EDP), problème de valeur limite surdéterminée, symétrique, nombres premiers, mécanique des fluides, géométrie, dérivées, analytique, euclidien, algébrique