Novel mathematical descriptions stay ahead of the curve
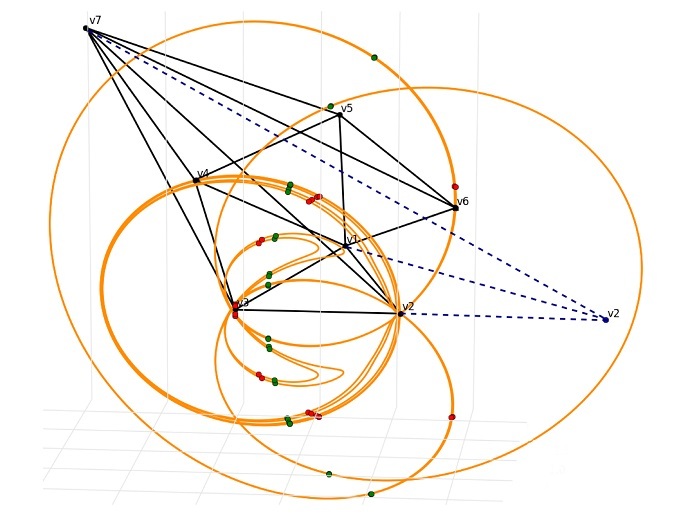
Mathematics – formally the study of numbers, shapes, and space – provides a language we use to describe the world around us. Geometry is the branch that focuses on the relationship between points, lines, curves, and surfaces. With the support of the Marie Skłodowska-Curie actions MCSA), the ISOPARAMETRIC project set out to investigate a specific class of surfaces (isoparametric hypersurfaces) that have attracted significant interest over the last couple decades.
Curving all around us
Project coordinator Alberto Enciso of the Institute of Mathematical Sciences – ICMAT explains: “Roughly speaking, an isoparametric hypersurface is a smooth geometric shape that curves itself in the same way everywhere. A circle, a plane, and the surface of a sphere or a cylinder are the most basic examples of isoparametric hypersurfaces. These objects are found in 2- and 3-dimensional space and are maximally symmetric – the objects look the same from a maximal number of different viewpoints.” Enciso continues with what happens on moving to higher dimensions. “We find very interesting and rather complicated isoparametric hypersurfaces that are not as symmetric as one might expect.” Isoparametric surfaces are found throughout physics and mathematics. For example, equilibrium shapes of self-gravitating fluids in fluid mechanics are isoparametric surfaces and there is an unexpected connection between prime numbers and related objects called isoparametric foliations. MCSA fellow Miguel Domínguez-Vázquez, now at the University of Santiago de Compostela, investigated these intriguing surfaces from various perspectives.
The solution to many problems
Many problems in science are modelled by partial differential equations (PDEs) involving derivatives, rates of change of one variable with respect to others. Some of these equations may not have solutions, as is the case of many overdetermined boundary value problems of PDEs, a key area of research over the last 50 years. The term ‘overdetermined’ means there are more equations than unknowns and so they often have no solution. Enciso and Domínguez-Vázquez advanced this important field: “Among our key outcomes was proving the existence of solutions to overdetermined boundary value problems of PDEs in very general contexts and showing that, under certain circumstances, such solutions are related to isoparametric hypersurfaces. Further, we developed a complete understanding of isoparametric (hyper)surfaces in certain important non-flat spaces of three dimensions, showing that in these cases isoparametric surfaces are indeed maximally symmetric.” ISOPARAMETRIC outcomes are expected to find future application in obtaining existence or non-existence results for isoparametric hypersurfaces in general, as well as enabling complete understanding of isoparametric surfaces in the so-called ‘homogeneous spaces of dimension 3’. They will likely also be used when dealing with incompressible fluid flows.
A new way of looking at isoparametric hypersurfaces
Isoparametric hypersurfaces have usually been investigated with algebraic and differential geometric methods, where classical differential geometry deals with curves and surfaces in the Euclidean 3D space. Domínguez-Vázquez concludes: “The most exciting thing about this project was initiating a new line of research that required learning about a different area of mathematics. ISOPARAMETRIC investigated isoparametric hypersurfaces and related objects by combining these ‘classical’ methods with more analytic techniques.” Clearly, a steep learning curve led to important outcomes regarding these intriguing surfaces that curve themselves in the same way everywhere.
Keywords
ISOPARAMETRIC, isoparametric hypersurfaces, mathematics, partial differential equations (PDEs), overdetermined boundary value problem, symmetric, prime numbers, fluid mechanics, geometric, geometry, derivatives, analytic, Euclidian, algebraic