Nowatorskie opisy matematyczne krzywych i powierzchni
Matematyka – formalnie nauka o liczbach, kształtach i przestrzeniach – stanowi język umożliwiający nam opisywanie otaczającego nas świata. Geometria to z kolei dziedzina matematyki, która skupia się na relacjach między punktami, liniami, krzywymi i powierzchniami. Projekt ISOPARAMETRIC, wspierany ze środków działania „Maria Skłodowska-Curie”(MSCA), miał na celu zbadanie specyficznej klasy powierzchni (hiperpowierzchni izoparametrycznych), które cieszą się dużym zainteresowaniem badaczy od kilkudziesięciu lat.
Krzywe wokół nas
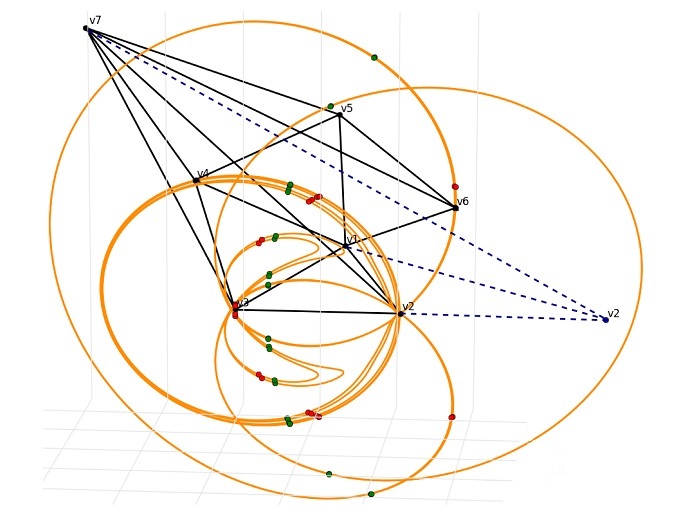
Koordynator projektu Alberto Enciso z Instytutu Nauk Matematycznych (ICMAT) wyjaśnia: „Mówiąc w uproszczeniu, hiperpowierzchnia izoparametryczna to gładki geometryczny kształt, który zakrzywia się w każdym miejscu w taki sam sposób. Okrąg, płaszczyzna i powierzchnia kuli lub walca to najbardziej podstawowe przykłady hiperpowierzchni izoparametrycznych. Obiekty te występują w przestrzeni dwu- i trójwymiarowej i są maksymalnie symetryczne – wyglądają identycznie z maksymalnej liczby różnych punktów widzenia”. Dalej Enciso tłumaczy, co dzieje się po przejściu do wyższych wymiarów. „Znajdujemy bardzo interesujące i dość skomplikowane hiperpowierzchnie izoparametryczne, które nie są tak symetryczne, jak można by się spodziewać”. Powierzchnie izoparametryczne są powszechne we wszystkich obszarach fizyki i matematyki. Powierzchniami izoparametrycznymi są na przykład kształty równowagowe płynów samograwitujących w mechanice płynów. Istnieje też nieoczekiwana zależność między liczbami pierwszymi a powiązanymi obiektami zwanymi foliacjami izoparametrycznymi. Stypendysta działania „Maria Skłodowska-Curie” Miguel Domínguez-Vázquez, pracujący obecnie na Uniwersytecie w Santiago de Compostela, badał te intrygujące powierzchnie z różnych perspektyw.
Rozwiązanie wielu problemów
Wiele problemów naukowych daje się modelować przy pomocy równań różniczkowych cząstkowych obejmujących pochodne, czyli wskaźniki zmiany jednej zmiennej w stosunku do innych. Niektóre z tych równań mogą nie mieć rozwiązań, jak to ma miejsce w przypadku wielu nadokreślonych problemów wartości granicznych równań różniczkowych cząstkowych, jednego z najważniejszych obszaru badań matematycznych ostatniego półwiecza. Termin „nadokreślony” oznacza, że liczba równań jest większa niż liczba niewiadomych i dlatego często nie mają one żadnego rozwiązania. Enciso i Domínguez-Vázquez wnieśli wkład w rozwój tej ważnej dziedziny: „Jednym z naszych najważniejszych osiągnięć było udowodnienie istnienia rozwiązań dla nadokreślonych problemów wartości granicznych równań różniczkowych cząstkowych w bardzo ogólnych kontekstach oraz wykazanie, że w pewnych okolicznościach takie rozwiązania są powiązane z hiperpowierzchniami izoparametrycznymi. Ponadto, dokonaliśmy kompletnej analizy (hiper)powierzchni izoparametrycznych w niektórych ważnych przestrzeniach niepłaskich o trzech wymiarach, dowodząc, że w tych przypadkach powierzchnie izoparametryczne są faktycznie maksymalnie symetryczne”. Rezultaty projektu ISOPARAMETRIC powinny znaleźć w przyszłości zastosowanie w poszukiwaniu istniejących lub nieistniejących wyników hiperpowierzchni izoparametrycznych, jak również umożliwią pełne zrozumienie powierzchni izoparametrycznych w tak zwanych „przestrzeniach jednorodnych trzeciego wymiaru”. Być może zostaną też wykorzystane do badania przepływów płynów nieściśliwych.
Nowy sposób patrzenia na hiperpowierzchnie izoparametryczne
Hiperpowierzchnie izoparametryczne były dotąd zwykle badane metodami algebraicznymi i różniczkowo-geometrycznymi (klasyczna geometria różniczkowa zajmuje się krzywymi i powierzchniami w trójwymiarowej przestrzeni euklidesowej). Domínguez-Vázquez podsumowuje: „Najbardziej ekscytującym aspektem projektu było zapoczątkowanie nowej linii badań, która wymagała od nas poznania innej dziedziny matematyki. W projekcie ISOPARAMETRIC badaliśmy hiperpowierzchnie izoparametryczne i obiekty pokrewne, łącząc te »klasyczne« metody z technikami bardziej analitycznymi”. Można powiedzieć, że stroma krzywa uczenia się pozwoliła nam na uzyskanie ważnych wyników w odniesieniu do tych intrygujących powierzchni, które zakrzywiają się w każdym miejscu w ten sam sposób.
Słowa kluczowe
ISOPARAMETRIC, hiperpowierzchnie izoparametryczne, matematyka, równania różniczkowe cząstkowe, nadokreślony problem wartości granicznych, symetryczne, liczby pierwsze, mechanika płynów, geometryczne, geometria, pochodne, analityczne, euklidesowe, algebraiczne