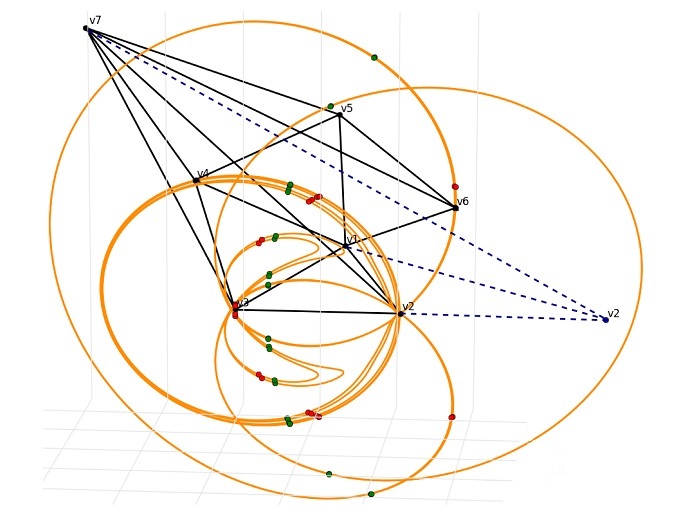
Geometryczna analiza równań opisujących zjawiska tego świata
Rozwiązywanie szczególnych równań może nieść ze sobą szereg potencjalnych możliwości dla matematyków, naukowców i inżynierów. Identyfikacja tych zastosowań często zajmuje jednak bardzo wiele czasu. Finansowany przez UE projekt GEOGRAL koncentruje się na szczególnej rodzinie równań, określanych jako równania różniczkowe cząstkowe (RRC), które mogą posłużyć do opisywania wielu z występujących na świecie zjawisk. „Równania różniczkowe cząstkowe (RRC) opisują praktycznie każde zjawisko występujące na świecie, w którym żyjemy” − mówi prof. Janusz Grabowski z Instytutu Matematycznego Polskiej Akademii Nauk. Wśród zjawisk tych znajdują się m.in. ekonomiczne zagadnienie optymalnego podziału zasobów, które opisywane jest przez tzw. równanie Monge’a-Ampere’a, odkryte niedawno fale grawitacyjne, które zostały przewidziane przez słynne równanie Einsteina, oraz współczesne metody prognozowania pogody, które opierają się na równaniach opisujących zachowanie płynów. „Równania RRC formalizują − z matematycznego punktu widzenia − fakt, że obecne zachowanie danego zjawiska jest wynikiem jego stanu w przeszłości” − kontynuuje prof. Grabowski. Typowym przykładem jest zastosowanie tych równań do opisania rozwoju populacji bakterii. Jeżeli początkowa populacja obejmuje jedną bakterię, to po 1 minucie będą w niej dwie bakterie, po 2 minutach − cztery, po 3 minutach − osiem itd., zgodnie z modelem wzrostu wykładniczego. Przyrost populacji zależeć będzie od czasu trwania procesu rozmnażania: na początku populacja zwiększa się zaledwie o kilka sztuk, jednak po godzinie może ona zawierać miliardy bakterii. Geometryczna charakterystyka równań RRC Celem badawczym projektu było odkrycie geometrycznej metody charakteryzowania tej szczególnej rodziny równań. Zastosowanie geometrii do równań RRC cieszy się długą tradycją, sięgającą początku dwudziestego wieku. Opracowanie metodologii geometrycznej mogłoby pozwolić matematykom odróżnić tę szczególną rodzinę od wszystkich innych równań. Jednakże uzyskanie umiejętności potrzebnych do wizualizacji równań RRC w postaci obiektów geometrycznych wymaga wielu lat pracy. Prowadzenie podstawowych badań w takich dziedzinach jest konieczne dla zagwarantowania postępu nauki, badań oraz inżynierii w oparciu o solidne matematyczne fundamenty. Poszukiwanie równań RRC wykazujących określone symetrie Proces odkrywania równań mogących potencjalnie wyjaśnić poszczególne zjawiska często wymaga od badaczy prowadzenia poszukiwań. W tym celu identyfikują oni określone „symetrie” wyrażane przez dane zjawisko, a następnie badają szereg równań RRC, dopóki nie odkryją równania, które wyraża takie same symetrie. Zespół projektu GEOGRAL pomyślnie opracował ogólną procedurę, która − przy założeniu dowolnej początkowej grupy symetrii − umożliwia zidentyfikowanie równania odzwierciedlającego dokładnie te same symetrie. Ponadto zespół projektu opublikował kilka opracowań, w których szczegółowo opisano wyniki badań pobocznych. „Wyniki te zdecydowanie potwierdzają możliwość skutecznego zastosowania geometrii do rozwiązywania zagadnień dotyczących równań RCC” − mówi prof. Grabowski. „Wyniki uzyskane w ramach projektu GEOGRAL stanowią źródło inspiracji dla doświadczonych, zawodowych matematyków oraz motywacji dla młodych adeptów matematyki rozważających rozpoczęcie kariery naukowej”. Jak stwierdza prof. Grabowski, w perspektywie długoterminowej „można przypuszczać, że głębsze zrozumienie równań RCC z punktu widzenia geometrii będzie pomocne w opisywaniu istotnych zjawisk fizycznych; być może − oby tak było − odbywać się to będzie w synergii z istniejącymi, zaawansowanymi metodami numerycznymi”.
Słowa kluczowe
GEOGRAL, geometria, matematyka, matematyka teoretyczna, równania różniczkowe cząstkowe, RRC